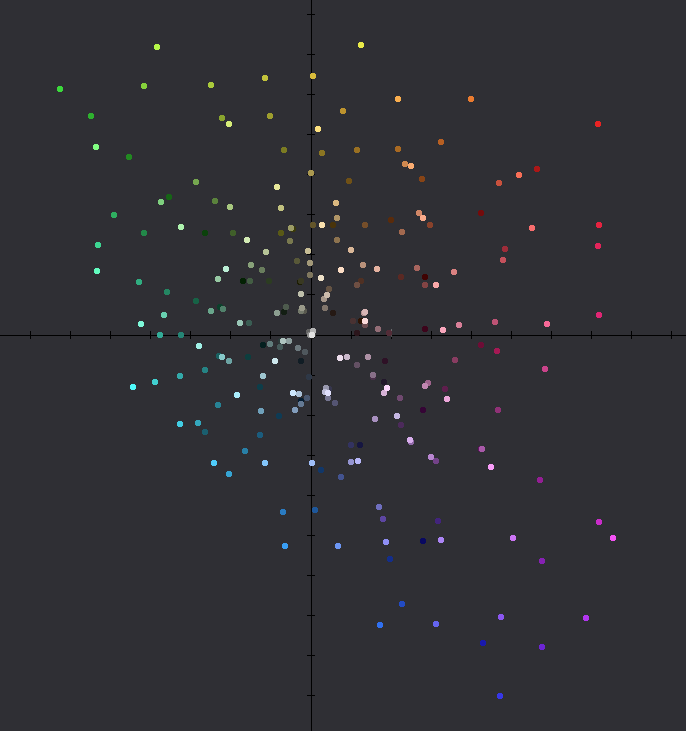
So I plotted all the 255 colors on a grid based on Lab coloration. I made layers to group together colors with similar L values. It helps to illustrate some of the space you have to traverse.Luminous yellow is out there, so it makes sense that it’s harder to mutate. I bet it’s impossible to mix. The best you could manage would be to mix it with some of the colors close to it and double up on the yellow. As long as you don’t crowd out the yellow. Same with all the extreme pointy ends.
for the goo mutation step, a graph has been generated that links all the colours together in a somewhat sensible way, and it steps through that graph to whichever neighbour is closest to the target than the current colour is; the random mutation then kicks in to sometimes also step it 1 neighbour in any direction.
the graph is generated by starting from each of the 255 colours, and evaluating for all the other 254 colours which of the 254 remaining colours in closest to the current colour, whilst also being closer to that other colour than the current colour is, and adding a link between those colours to the graph. Basically ensuring that no matter which colour it is morphing towards in the goo mutation (aka the 255 gleam colours) there is always a step you can take in the graph that brings you closer to the target than the current colour is and that those steps are somewhat minimal in distance.
Distance here, is measured using the CIEDE2000 colour distance metric.
Colour mixing is a linear combination of the colours in the Lab color space, and then the result is mapped to the closest in the palette, again with the CIEDE2000 colour distance metric.
This is great information! Thanks @lucadeltodecso!
So, if we ignore L (the unseen third dimension in this graph) then we could expect mutation between the two colors in the left image to step through along a path somewhat like what is shown in the second (depending on whether there is a bias to step distance increments or not). While mixing equal amounts of the two colors of pigment would likely return the color in the magenta circle, since it’s roughly equidistant between the two initial colors.


I’m curious how mixing would work between two colors with no other colors reasonably between them. For example, if we mix the two colors shown below in equal parts, which color spray will we get? Do we break ties based on stack order in the mixer? As in most left pigment wins?

Trust that I will do some testing ![]()
![]()
you wouldnt get the magenta circled one most likely, it is taking the weighted average of the colours, then picking the “nearest” colour, which is going to be one of those two extra that you circled in white instead.
In the bottom case with no colours closer than the two inputs, you would never be able to get anything other than one of those two colours as output. the “breaking ties” case if the inputs were equal in count is likely just going to be whichever has the smallest color-index
Yeah, after I posted that, I realized it was more likely to go along the grey line. That’s what I get for summarizing complex color theory while at work!
I hadn’t thought of color index!
Thanks! 
So I did a bunch of work using this article: https://en.wikipedia.org/wiki/Color_difference and I put together a Google Sheets doc that attempts to calculate color difference between two colors. The hope being that I can move this in to something that would allow me to predict mix results as well as plan mutation strategies a bit better.
https://docs.google.com/spreadsheets/d/1V2jhSLnXfFDhTh_szHy0ebOTLjmj9CEe1W3D9EH97z0/edit?usp=sharing
However, when I calculate the difference between Vivid Green and Turquoise using my sheet, I get a difference of 30.02, but when I use the calculator here http://brucelindbloom.com/index.html?ColorDifferenceCalc.html, which I trust much more than my own work, I get a result of 31.41. Further, I KNOW that mixing Vivid Green and Turquoise in equal parts should return Mint, and I’m seeing that Warm Viridian is closer to each of them.
My suspicion is that I’ve messed up when it comes to the kC and kH variables, which I assumed would be 1 like kL. But maybe even kL isn’t 1.
I’d love some help from my fellow mathers! Apologies for the mess in the file, I splayed everything out to try and understand each part better.
If all this is needed to play this part of the game you can count me out. Glad someone is doing the maths though.
I’ll be cheering for you to figure it out @Firehazurd
It’s not needed, I’m just a big numbers nerd and like being able to plan things out!
That being said, if you’ve got a stash of goo kernels you don’t want…
Me and @Simoyd tried to figure that out when testing came out and we were always off for some colors. Maybe with the new info that as been given out we could give it a second try.
There are definitely levers that end users can manipulate to affect their color progression. So it might just be that we’ll never be able to infer those levers.
But if you guys DO start messing with it again, let me know!
Oops, I just realized my sheet was locked or something and that others might not be able to access it. It should be open now.
A few quick checks, your Lab values for the colors in the palette are not correct, they’re somewhat subtly wrong (at least for the first 5 I checked, it not being ordered 1-255 didnt help!) perhaps missing a conversion from sRGB? (the palette hex values are sRGB)
here’s a dump of the exact Lab values the game uses for the palette colours for colour mixing:
Summary
[2019-08-23 00:19:31.544] [INFO] 9.76693 0.00116851 -0.00231196
[2019-08-23 00:19:31.544] [INFO] 10.0419 -2.52559 -7.11821
[2019-08-23 00:19:31.544] [INFO] 10.117 -0.245472 -16.5691
[2019-08-23 00:19:31.544] [INFO] 23.217 0.0841303 -10.6027
[2019-08-23 00:19:31.544] [INFO] 23.5335 6.08582 -14.0589
[2019-08-23 00:19:31.544] [INFO] 23.5436 8.56829 -5.91298
[2019-08-23 00:19:31.544] [INFO] 23.4405 16.9292 -11.35
[2019-08-23 00:19:31.544] [INFO] 23.498 25.4244 -23.2033
[2019-08-23 00:19:31.544] [INFO] 23.4189 45.3385 -28.3557
[2019-08-23 00:19:31.544] [INFO] 23.3289 35.1909 -13.9186
[2019-08-23 00:19:31.544] [INFO] 23.2342 42.8406 1.971
[2019-08-23 00:19:31.544] [INFO] 23.2146 35.4249 14.9003
[2019-08-23 00:19:31.544] [INFO] 23.2737 21.8917 14.4279
[2019-08-23 00:19:31.544] [INFO] 23.3297 12.4859 14.1682
[2019-08-23 00:19:31.544] [INFO] 23.4318 10.433 4.15001
[2019-08-23 00:19:31.544] [INFO] 23.2404 19.077 0.651001
[2019-08-23 00:19:31.544] [INFO] 10.0046 28.3181 1.03827
[2019-08-23 00:19:31.544] [INFO] 9.96656 18.2427 -7.66224
[2019-08-23 00:19:31.544] [INFO] 10.0233 12.186 0.636473
[2019-08-23 00:19:31.544] [INFO] 10.1002 5.10525 5.73537
[2019-08-23 00:19:31.544] [INFO] 9.88562 12.1134 13.8288
[2019-08-23 00:19:31.544] [INFO] 10.0188 28.1275 14.5083
[2019-08-23 00:19:31.544] [INFO] 23.4531 42.1685 30.0785
[2019-08-23 00:19:31.544] [INFO] 36.6169 56.3211 40.7069
[2019-08-23 00:19:31.544] [INFO] 36.6794 47.5058 19.9345
[2019-08-23 00:19:31.544] [INFO] 36.7 26.9143 12.2128
[2019-08-23 00:19:31.544] [INFO] 36.6927 14.1357 2.9954
[2019-08-23 00:19:31.544] [INFO] 36.5786 11.2805 12.2159
[2019-08-23 00:19:31.544] [INFO] 36.5576 4.36979 12.0046
[2019-08-23 00:19:31.544] [INFO] 36.7393 12.424 27.6292
[2019-08-23 00:19:31.544] [INFO] 36.72 6.97245 37.6374
[2019-08-23 00:19:31.544] [INFO] 36.5873 -0.370444 26.9289
[2019-08-23 00:19:31.544] [INFO] 36.6302 -5.66933 18.5984
[2019-08-23 00:19:31.544] [INFO] 36.6055 -9.12359 36.6735
[2019-08-23 00:19:31.544] [INFO] 36.8209 -21.9101 26.5024
[2019-08-23 00:19:31.544] [INFO] 36.6362 -39.1233 35.4884
[2019-08-23 00:19:31.544] [INFO] 23.2569 -29.1605 26.4433
[2019-08-23 00:19:31.544] [INFO] 23.2797 -12.2964 14.0232
[2019-08-23 00:19:31.544] [INFO] 23.377 -4.35107 14.3661
[2019-08-23 00:19:31.544] [INFO] 23.5048 -6.86164 27.5938
[2019-08-23 00:19:31.544] [INFO] 23.3267 4.92719 27.9745
[2019-08-23 00:19:31.544] [INFO] 23.2825 1.68597 13.7609
[2019-08-23 00:19:31.544] [INFO] 9.95691 1.67158 13.6809
[2019-08-23 00:19:31.544] [INFO] 10.1568 -4.57067 13.8398
[2019-08-23 00:19:31.544] [INFO] 9.90724 -7.86992 5.83466
[2019-08-23 00:19:31.544] [INFO] 9.83497 -10.138 -3.05883
[2019-08-23 00:19:31.544] [INFO] 23.227 -5.71185 -1.89571
[2019-08-23 00:19:31.544] [INFO] 26.2074 0.00191407 -0.00378709
[2019-08-23 00:19:31.544] [INFO] 36.4971 -1.73804 -4.54775
[2019-08-23 00:19:31.544] [INFO] 41.9647 0.00262865 -0.00520092
[2019-08-23 00:19:31.544] [INFO] 36.703 -2.02019 5.81454
[2019-08-23 00:19:31.544] [INFO] 36.7918 -7.91534 5.82586
[2019-08-23 00:19:31.544] [INFO] 36.7942 -15.588 11.8769
[2019-08-23 00:19:31.544] [INFO] 36.6548 -15.1982 1.7427
[2019-08-23 00:19:31.544] [INFO] 36.775 -20.9834 -6.29233
[2019-08-23 00:19:31.544] [INFO] 36.6511 -14.9619 -15.1454
[2019-08-23 00:19:31.544] [INFO] 36.6833 -8.13602 -24.333
[2019-08-23 00:19:31.544] [INFO] 36.791 6.72248 -41.7809
[2019-08-23 00:19:31.544] [INFO] 36.674 11.8444 -35.2162
[2019-08-23 00:19:31.544] [INFO] 36.7069 0.923368 -15.4817
[2019-08-23 00:19:31.544] [INFO] 36.8187 7.2989 -17.0942
[2019-08-23 00:19:31.544] [INFO] 36.5383 11.662 -8.04162
[2019-08-23 00:19:31.544] [INFO] 36.5411 23.013 -15.412
[2019-08-23 00:19:31.544] [INFO] 36.5911 33.9484 -30.7759
[2019-08-23 00:19:31.544] [INFO] 36.5859 32.4358 -46.7074
[2019-08-23 00:19:31.544] [INFO] 36.7029 65.0753 -76.4579
[2019-08-23 00:19:31.544] [INFO] 36.7633 62.401 -56.3171
[2019-08-23 00:19:31.544] [INFO] 36.6732 60.2108 -37.6774
[2019-08-23 00:19:31.544] [INFO] 36.6389 47.426 -19.2443
[2019-08-23 00:19:31.544] [INFO] 36.6102 36.8296 -6.17309
[2019-08-23 00:19:31.544] [INFO] 36.6209 57.444 2.74559
[2019-08-23 00:19:31.544] [INFO] 49.9992 46.3786 2.1609
[2019-08-23 00:19:31.544] [INFO] 49.9847 59.5782 -10.2591
[2019-08-23 00:19:31.544] [INFO] 50.0904 72.0909 3.63722
[2019-08-23 00:19:31.544] [INFO] 49.8949 71.4444 19.3181
[2019-08-23 00:19:31.544] [INFO] 50.1302 47.2527 17.517
[2019-08-23 00:19:31.544] [INFO] 49.972 71.1284 35.1778
[2019-08-23 00:19:31.544] [INFO] 50.0723 70.7779 51.2149
[2019-08-23 00:19:31.544] [INFO] 50.0984 46.2106 35.6731
[2019-08-23 00:19:31.544] [INFO] 50.0259 26.1798 15.4918
[2019-08-23 00:19:31.544] [INFO] 50.0424 20.3026 24.1682
[2019-08-23 00:19:31.544] [INFO] 50.1538 9.38239 15.2092
[2019-08-23 00:19:31.544] [INFO] 50.0836 5.06169 23.7339
[2019-08-23 00:19:31.544] [INFO] 50.1135 -1.23198 14.885
[2019-08-23 00:19:31.544] [INFO] 49.863 -7.04762 23.082
[2019-08-23 00:19:31.544] [INFO] 50.0503 -13.6894 15.0917
[2019-08-23 00:19:31.544] [INFO] 50.1106 -21.5474 6.81885
[2019-08-23 00:19:31.544] [INFO] 50.0407 -31.3323 0.668941
[2019-08-23 00:19:31.544] [INFO] 49.8665 -36.9146 11.4651
[2019-08-23 00:19:31.544] [INFO] 50.0129 -43.3643 25.7417
[2019-08-23 00:19:31.544] [INFO] 49.9074 -48.9899 44.6993
[2019-08-23 00:19:31.544] [INFO] 50.0555 -27.0097 33.1884
[2019-08-23 00:19:31.544] [INFO] 50.0879 -11.4557 46.0286
[2019-08-23 00:19:31.544] [INFO] 49.8904 -0.663605 46.3559
[2019-08-23 00:19:31.544] [INFO] 50.0686 8.69805 47.0583
[2019-08-23 00:19:31.544] [INFO] 50.1488 19.4745 47.7858
[2019-08-23 00:19:31.544] [INFO] 49.9385 31.4137 48.3371
[2019-08-23 00:19:31.544] [INFO] 63.23 37.8967 57.8379
[2019-08-23 00:19:31.544] [INFO] 63.2439 21.5499 41.2088
[2019-08-23 00:19:31.544] [INFO] 63.2291 24.9104 28.8854
[2019-08-23 00:19:31.544] [INFO] 63.2156 11.4082 17.8161
[2019-08-23 00:19:31.544] [INFO] 63.405 3.31131 8.84692
[2019-08-23 00:19:31.544] [INFO] 63.1907 -2.92543 8.40178
[2019-08-23 00:19:31.544] [INFO] 63.3011 -1.58445 18.1739
[2019-08-23 00:19:31.544] [INFO] 63.4577 3.47307 28.5136
[2019-08-23 00:19:31.544] [INFO] 63.3591 -3.02338 40.3859
[2019-08-23 00:19:31.544] [INFO] 63.1807 -8.61517 28.3331
[2019-08-23 00:19:31.544] [INFO] 63.4291 -16.3445 18.0133
[2019-08-23 00:19:31.544] [INFO] 63.3068 -9.51014 5.04661
[2019-08-23 00:19:31.544] [INFO] 63.445 -5.99091 -2.05153
[2019-08-23 00:19:31.544] [INFO] 57.8642 0.00334968 -0.00662752
[2019-08-23 00:19:31.544] [INFO] 50.0163 -3.33844 -4.25422
[2019-08-23 00:19:31.544] [INFO] 49.992 -9.66822 -3.20756
[2019-08-23 00:19:31.544] [INFO] 50.0366 -4.62977 7.03219
[2019-08-23 00:19:31.544] [INFO] 50.0389 2.84459 7.19114
[2019-08-23 00:19:31.544] [INFO] 50.0354 16.5345 0.91696
[2019-08-23 00:19:31.544] [INFO] 49.9546 14.4978 -10.0002
[2019-08-23 00:19:31.544] [INFO] 49.9877 30.1134 -12.6577
[2019-08-23 00:19:31.544] [INFO] 49.8541 43.9706 -28.695
[2019-08-23 00:19:31.544] [INFO] 50.0892 27.4355 -27.3878
[2019-08-23 00:19:31.544] [INFO] 50.1089 20.3778 -42.071
[2019-08-23 00:19:31.544] [INFO] 49.9363 39.3178 -70.201
[2019-08-23 00:19:31.544] [INFO] 50.0205 54.7358 -69.9145
[2019-08-23 00:19:31.544] [INFO] 49.9712 75.4088 -69.7753
[2019-08-23 00:19:31.544] [INFO] 50.0206 75.6129 -47.3075
[2019-08-23 00:19:31.544] [INFO] 63.3756 79.8921 -50.5348
[2019-08-23 00:19:31.544] [INFO] 63.2773 55.4302 -51.0379
[2019-08-23 00:19:31.544] [INFO] 63.457 37.9946 -50.9674
[2019-08-23 00:19:31.544] [INFO] 63.4066 24.8784 -51.2014
[2019-08-23 00:19:31.544] [INFO] 63.4083 13.739 -31.2364
[2019-08-23 00:19:31.544] [INFO] 63.3701 18.0551 -21.0738
[2019-08-23 00:19:31.544] [INFO] 63.3164 32.9424 -31.1141
[2019-08-23 00:19:31.544] [INFO] 63.2102 28.8224 -13.1817
[2019-08-23 00:19:31.544] [INFO] 63.3148 14.3533 -6.43711
[2019-08-23 00:19:31.545] [INFO] 63.2426 12.7688 4.82932
[2019-08-23 00:19:31.545] [INFO] 76.6686 12.5836 4.70183
[2019-08-23 00:19:31.545] [INFO] 76.7013 16.015 16.3136
[2019-08-23 00:19:31.545] [INFO] 76.6235 25.799 28.416
[2019-08-23 00:19:31.545] [INFO] 76.6919 22.5007 41.6449
[2019-08-23 00:19:31.545] [INFO] 76.7675 19.1459 58.6828
[2019-08-23 00:19:31.545] [INFO] 76.5523 9.22565 65.8182
[2019-08-23 00:19:31.545] [INFO] 76.6996 -3.09455 65.314
[2019-08-23 00:19:31.545] [INFO] 76.6476 -16.0716 64.6122
[2019-08-23 00:19:31.545] [INFO] 76.7413 -29.836 64.0814
[2019-08-23 00:19:31.545] [INFO] 76.6204 -46.8738 63.2452
[2019-08-23 00:19:31.545] [INFO] 76.601 -68.8193 62.4217
[2019-08-23 00:19:31.545] [INFO] 76.7735 -41.0294 32.6188
[2019-08-23 00:19:31.545] [INFO] 76.7762 -55.1348 22.4004
[2019-08-23 00:19:31.545] [INFO] 76.7936 -37.87 6.67
[2019-08-23 00:19:31.545] [INFO] 76.6772 -23.966 13.7716
[2019-08-23 00:19:31.545] [INFO] 76.7612 -18.0988 3.16198
[2019-08-23 00:19:31.545] [INFO] 76.7145 -21.0411 -6.7505
[2019-08-23 00:19:31.545] [INFO] 76.5514 -36.7601 -11.0251
[2019-08-23 00:19:31.545] [INFO] 76.6198 -29.8444 -21.6823
[2019-08-23 00:19:31.545] [INFO] 76.8083 -20.1695 -32.6335
[2019-08-23 00:19:31.545] [INFO] 76.7185 -6.95813 -32.6174
[2019-08-23 00:19:31.545] [INFO] 76.7017 3.54041 -32.5116
[2019-08-23 00:19:31.545] [INFO] 76.5418 14.103 -32.6225
[2019-08-23 00:19:31.545] [INFO] 76.8171 13.2403 -19.6936
[2019-08-23 00:19:31.545] [INFO] 76.6551 5.32935 -13.5175
[2019-08-23 00:19:31.545] [INFO] 76.7406 9.60918 -6.75202
[2019-08-23 00:19:31.545] [INFO] 76.6741 19.1832 -13.2576
[2019-08-23 00:19:31.545] [INFO] 76.7627 26.7727 -25.5668
[2019-08-23 00:19:31.545] [INFO] 76.636 34.0232 -15.7966
[2019-08-23 00:19:31.545] [INFO] 76.7355 47.9575 -31.8159
[2019-08-23 00:19:31.545] [INFO] 63.3909 56.179 -23.8138
[2019-08-23 00:19:31.545] [INFO] 63.2677 58.9578 2.51555
[2019-08-23 00:19:31.545] [INFO] 63.3798 37.3972 1.57595
[2019-08-23 00:19:31.545] [INFO] 63.5004 34.2742 14.87
[2019-08-23 00:19:31.545] [INFO] 63.3411 53.2328 26.6843
[2019-08-23 00:19:31.545] [INFO] 63.354 50.8504 38.9309
[2019-08-23 00:19:31.545] [INFO] 76.7737 30.2075 12.3925
[2019-08-23 00:19:31.545] [INFO] 76.7051 33.5281 1.35753
[2019-08-23 00:19:31.545] [INFO] 90.0098 19.0791 -13.2404
[2019-08-23 00:19:31.545] [INFO] 90.0269 7.74536 -5.472
[2019-08-23 00:19:31.545] [INFO] 89.946 5.30581 -13.57
[2019-08-23 00:19:31.545] [INFO] 90.0722 -4.02597 -13.5266
[2019-08-23 00:19:31.545] [INFO] 89.9732 -7.32366 -5.81448
[2019-08-23 00:19:31.545] [INFO] 89.874 -17.6135 -14.0349
[2019-08-23 00:19:31.545] [INFO] 76.7421 -10.6737 -9.27248
[2019-08-23 00:19:31.545] [INFO] 76.7912 -7.91263 -0.427259
[2019-08-23 00:19:31.545] [INFO] 74.0478 0.00408359 -0.0080796
[2019-08-23 00:19:31.545] [INFO] 76.7864 3.0112 10.1408
[2019-08-23 00:19:31.545] [INFO] 76.7029 8.0806 20.4659
[2019-08-23 00:19:31.545] [INFO] 76.5242 4.68193 32.9742
[2019-08-23 00:19:31.545] [INFO] 76.5208 -2.69296 21.0213
[2019-08-23 00:19:31.545] [INFO] 76.7692 -3.87281 9.97168
[2019-08-23 00:19:31.545] [INFO] 76.7129 -12.6119 21.0611
[2019-08-23 00:19:31.545] [INFO] 76.7793 -23.2485 33.0649
[2019-08-23 00:19:31.545] [INFO] 76.6849 -10.1149 33.2906
[2019-08-23 00:19:31.545] [INFO] 90.0635 -11.5614 38.0402
[2019-08-23 00:19:31.545] [INFO] 89.9617 -24.489 53.6518
[2019-08-23 00:19:31.545] [INFO] 89.9536 -44.6836 72.8383
[2019-08-23 00:19:31.545] [INFO] 90.0922 -58.7324 48.5774
[2019-08-23 00:19:31.545] [INFO] 89.9316 -34.5951 26.579
[2019-08-23 00:19:31.545] [INFO] 90.051 -17.6764 24.022
[2019-08-23 00:19:31.545] [INFO] 90.0993 -21.1933 6.77581
[2019-08-23 00:19:31.545] [INFO] 89.9045 -27.0067 -2.54946
[2019-08-23 00:19:31.545] [INFO] 90.128 -41.5611 4.3745
[2019-08-23 00:19:31.545] [INFO] 89.8496 -54.6456 17.3014
[2019-08-23 00:19:31.545] [INFO] 89.9768 -42.1725 -12.6447
[2019-08-23 00:19:31.545] [INFO] 63.2968 -31.5129 -9.45055
[2019-08-23 00:19:31.545] [INFO] 63.3651 -17.9644 -5.76479
[2019-08-23 00:19:31.545] [INFO] 63.3773 -24.2802 -20.5104
[2019-08-23 00:19:31.545] [INFO] 63.3746 -15.265 -32.7606
[2019-08-23 00:19:31.545] [INFO] 63.3976 -9.581 -18.6006
[2019-08-23 00:19:31.545] [INFO] 63.3693 -2.01199 -19.1055
[2019-08-23 00:19:31.545] [INFO] 63.3239 12.5166 -51.4683
[2019-08-23 00:19:31.545] [INFO] 63.2231 -0.128261 -51.2047
[2019-08-23 00:19:31.545] [INFO] 50.107 0.386872 -43.4414
[2019-08-23 00:19:31.545] [INFO] 49.9574 -12.0279 -28.0922
[2019-08-23 00:19:31.545] [INFO] 50.1383 -19.9897 -17.3251
[2019-08-23 00:19:31.545] [INFO] 49.8482 -25.9221 -8.40047
[2019-08-23 00:19:31.545] [INFO] 63.3745 -37.6491 0.727497
[2019-08-23 00:19:31.545] [INFO] 63.4582 -25.9278 7.78966
[2019-08-23 00:19:31.545] [INFO] 63.404 -44.5725 13.5344
[2019-08-23 00:19:31.545] [INFO] 63.4327 -52.0243 30.7946
[2019-08-23 00:19:31.545] [INFO] 63.2011 -58.8714 53.403
[2019-08-23 00:19:31.545] [INFO] 63.3295 -32.3316 39.8807
[2019-08-23 00:19:31.545] [INFO] 63.3978 -25.8294 54.8911
[2019-08-23 00:19:31.545] [INFO] 63.2768 -13.7561 55.3153
[2019-08-23 00:19:31.545] [INFO] 63.2465 5.94071 56.2951
[2019-08-23 00:19:31.545] [INFO] 89.9824 -2.58576 51.0949
[2019-08-23 00:19:31.545] [INFO] 90.0094 0.971291 27.5254
[2019-08-23 00:19:31.545] [INFO] 89.951 0.392316 13.8205
[2019-08-23 00:19:31.545] [INFO] 90.063 7.07561 15.7111
[2019-08-23 00:19:31.545] [INFO] 90.0785 11.408 4.20511
[2019-08-23 00:19:31.545] [INFO] 89.8837 0.00480173 -0.00950049
[2019-08-23 00:19:31.545] [INFO] 76.7398 -2.77517 -13.5154
[2019-08-23 00:19:31.545] [INFO] 63.4658 4.29263 -10.9303
[2019-08-23 00:19:31.545] [INFO] 50.1186 5.97577 -14.6415
[2019-08-23 00:19:31.545] [INFO] 50.0859 -1.16879 -16.5725
[2019-08-23 00:19:31.545] [INFO] 50.1065 25.4631 -70.042
[2019-08-23 00:19:31.545] [INFO] 36.5789 31.1544 -66.4163
[2019-08-23 00:19:31.545] [INFO] 36.6886 57.3812 -87.5207
[2019-08-23 00:19:31.545] [INFO] 23.2724 51.6107 -74.7447
[2019-08-23 00:19:31.545] [INFO] 23.4644 27.341 -53.5981
[2019-08-23 00:19:31.545] [INFO] 23.2419 6.8788 -33.0297
[2019-08-23 00:19:31.545] [INFO] 23.2355 -5.00092 -19.3357
[2019-08-23 00:19:31.545] [INFO] 23.378 -10.8025 -11.8343
[2019-08-23 00:19:31.545] [INFO] 23.266 -15.6019 -4.67905
[2019-08-23 00:19:31.545] [INFO] 23.4031 -22.7251 8.10985
[2019-08-23 00:19:31.545] [INFO] 9.90441 -18.2014 13.2205
[2019-08-23 00:19:31.545] [INFO] 36.6679 -29.868 9.58048
[2019-08-23 00:19:31.545] [INFO] 36.6545 -7.58644 -2.51951
[2019-08-23 00:19:31.545] [INFO] 23.4538 13.5508 -27.3854
[2019-08-23 00:19:31.545] [INFO] 10.0002 15.3198 -27.4332
[2019-08-23 00:19:31.545] [INFO] 9.92666 34.2804 -49.5625
[2019-08-23 00:19:31.545] [INFO] 23.2546 35.4333 -45.0022
[2019-08-23 00:19:31.545] [INFO] 9.97262 29.7854 -18.6332
[2019-08-23 00:19:31.545] [INFO] 10.0098 10.516 -11.4584
[2019-08-23 00:19:31.545] [INFO] 23.2564 18.6879 28.6709
[2019-08-23 00:19:31.545] [INFO] 36.6366 25.3616 38.7028
[2019-08-23 00:19:31.545] [INFO] 36.7231 28.3687 27.747
[2019-08-23 00:19:31.545] [INFO] 89.8915 -18.3827 73.9453
That was very helpful! Thanks!
I updated all the Lab colors, and I’m definitely still getting some odd results. I think I need to comb back through all the variables!!!
Good luck I am cheering for you at least and sorry though I did learn higher math I was never good at anything except statistics :3 Trust me I would only make it worse if I tried to help ya ^^’
Will try to do some mixing experiments this weekend if I have any insights I will share them here with you.
I have another uneducated question, but it might help give a brute force solution to the colour dilemma at least until an acurate theoretical method for prediction is available…
Does pigment colour mixing follow the same prediction pathway as goo plant mutation mechanics? If so, a few volunteers each with say 20 pigments of their own specific colour could craft-and-stop in a binary search pattern to develop a rough but close colour disc…
Impossible
Color mixing is broken.
Lol its not, its just working on another system. Keep reading this thread you ll find it out or wait until we made some progress in research lol :3
Yeah, my utility is just straight not working. I’m getting bad results on the cookie difference, and then for the mix result, I’m average all the distances to find the smallest, which is definitely wrong.
I’m beginning to suspect it has to do with how I’m converting radians to degrees.